A common problem encountered by air travelers is the determination of the shortest way to fly from one city to another when a direct flight does not exist. Next we develop an algorithm that solves this and similar problems. First, let’s informally review some graph theory.
Graph Theory
Terminology
| 용어구분 | 설명 |
|---|---|
| vertex, node | 정점 |
| edge, arc | 이음선 |
| directed graph, digraph | 방향 그래프 |
| weight | 가중치 |
| simple path | 단순경로 (같은 정점을 두 번 지나지 않음) |
| path | 경로 (두 정점사이에 edge가 있는 정점들의 나열) |
| cycle | 순환 (한 정점에서 다시 그 정점으로 돌아오는 경로) |
| cyclic graph | 순환 그래프 |
| acyclic graph | 비순환 그래프 |
| weighted graph | 가중치 포함 그래프 |
| length | 길이 (weighted graph) the sum of weights on the path (unweighted graph) the number of edges on the path |
Weighted Graph
a weighted graph containing n vertices by an array W where
$$
W[i][j] =
\begin{cases}
\text{weight on edge} & \text{if there is an edge from $v_i$ to $v_j$} \\
\infty & \text{if there is no edge from $v_i$ to $v_j$}\\
0 & i=j
\end{cases}
$$
플로이드 알고리즘은 인풋과 아웃풋으로 그래프를 사용하기 때문에 그래프 자료구조에 대한 이해가 필요하다.
Floyd’s Algorithm for Shortest Paths using Dynamic Programming

- $W$ represents the graph in the above figure.
- $D$ contains the lengths of the shortest paths.
- $D^{(k)}[i][j]$ = length of a shortest path from $v_i$ to $v_j$ using only vertices in the set {$v_1, v_2, \cdots, v_k$} as intermediate vertices.
$W$는 그래프의 인접행렬을, $D$는 그래프 상 정점들 간의 최단경로 길이를 나타낸다.
$D^{(k)}[i][j]$는 {$v_1, v_2 , …, v_k$}의 정점들 만을 통해서 $v_i$에서 $v_j$로 가는 최단경로의 길이이다.
Algorithm Design
- Establish a recursive property (process) with which we can compute $D^{(k)}$ from $D^{(k-1)}$.
$$
\begin{align}
D^{(k)}[i][j] = minimum(& D^{(k-1)}[i][j], && \text{Case 1} \\
& D^{(k-1)}[i][k] + D^{(k-1)}[k][j]) && \text{Case 2}
\end{align}
$$
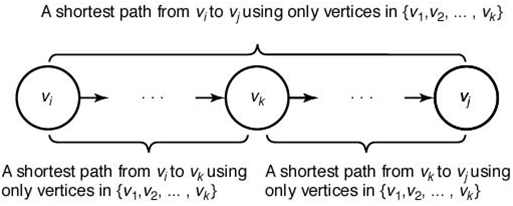
Case 1 At least one shortest path from $v_i$ to $v_j$ using only vertices in the set {$v_1, v_2, \cdots, v_k$} as intermediate vertices, does not use $v_k$.
Case 2 All shortest paths from $v_i$ to $v_j$, using only vertices in the set {$v_1, v_2, \cdots, v_k$} as intermediate vertices, do use $v_k$.
- Solve an instance of the problem in a bottom-up fashion by repeating the process (established in Step 1) for k =1 to n.
$D^{(0)}[2][5]$는 중간 정점으로 아무것도 지나지 않고 $v_2$에서 $v_5$로 가는 최단경로의 길이이다. 위의 인접행렬에서 확인할 수 있듯이 그 값은 $\infty$이다.
$D^{(1)}[2][5]$는 $v_2$에서 $v_1$을 거쳐 $v_5$로 가는 최단경로의 길이를 나타내며 그 값은 14이다. ($v_2$ $\rightarrow$ $v_1$ $\rightarrow$ $v_5$)
그래프 상의 어떤 정점도 중간 정점으로 이용하지 않는 $D^{(0)}$은 $W$와 동일하다. 반면 그래프 상의 모든 정점을 중간 정점으로 이용하는 $D^{(n)}$이 구하고자 하는 최종해($D$)이다.($D^{(0)} = W, \ D^{(n)} = D$)
결국 정점들의 개수가 n개이면 $D^{(0)}, D^{(1)}, \cdots, D^{(n)}$ 값을 계산해 나가고, $D = D^{(n)}$이 구하고자 하는 모든 정점들 사이의 최단 경로가 된다.
Pseudo Code
void floyd(const size_t n, const graph& g, int** D, int** P); |
Source Code
|
// File: floyd.cpp |
// File: floydtest.cpp |
Time Complexity Analysis
Basic operation
- The instruction in the for-j loop.
Input size
- n, the number of vertices in the graph. We have a loop within a loop within a loop, with n passes through each loop.
Every-Case Time Complexity
- $T(n) = n \times n \times n \in \Theta (n^3)$
Optimization Problem
The Shortest Paths problem is an optimization problem. There can be more than one candidate solution to an instance of an optimization problem. Each candidate solution has a value associated with it, and a solution to the instance is any candidate solution that has an optimal value. A candidate solution is a path from one vertex to another, the value is the length of the path, and the optimal value is the minimum of these lengths.
주어진 문제에 대하여 하나 이상의 많은 해답이 존재할 때, 이 가운데에서 가장 최적인 해답(optimal solution)을 찾아야 하는 문제를 최적화문제(optimization problem)라고 한다. 최단경로 찾기 문제는 최적화문제에 속한다.
Principle of Optimality
In case of the Shortest Paths problem we showed that if $v_k$ is a vertex on an optial path from $v_i$ to $v_j$, then the subpaths from $v_i$ to $v_k$ and from $v_k$ to $v_j$ must also be optmimal. Therefore, the optimal solution to the instance contains optimal solutions to all subinstances, and the principle of optimality applies.
최단경로를 구하는 문제에서, $v_k$를 $v_i$에서 $v_j$로 가는 최적 경로 상의 정점이라고 하면, $v_i$에서 $v_k$로 가는 부분경로와 $v_k$에서 $v_j$로 가는 부분경로도 반드시 최적이어야 한다. 이렇게 되면 최적의 원칙을 준수하게 되므로 동적계획법을 사용하여 이 문제를 풀 수 있다.
Dynamic Programming Exercises
Use Floyd’s algorithm for Shortest Paths problem to construct the matrix D, which contains the lengths of the shortest paths, and the matrix P, which contains the highest indices of the intermediate vertices on the shortest paths, for the following graph.
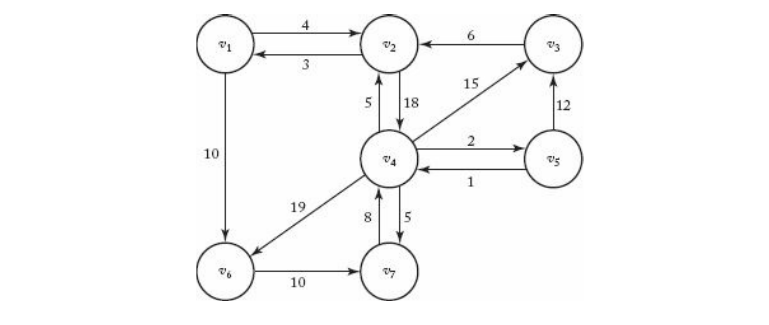
/* adjacency matrix for the above graph */ |
/* matrix D, which contains the lengths of the shortest paths */ |